“How Many Triangles are There” – a brainstorming and head-scratching puzzle is nowadays very popular in friend circles. Everybody tries hard to figure out all the triangles and claims that his/her answer is correct, no doubt about it 🙂.
But, this puzzle is actually one kind of illusion-related puzzles which makes too much illusion. This is why everybody cannot answer perfectly.
Anyhow,
There are three popular patterns:
| Pattern 1 | Pattern 2 | Pattern 3 |
|---|---|---|
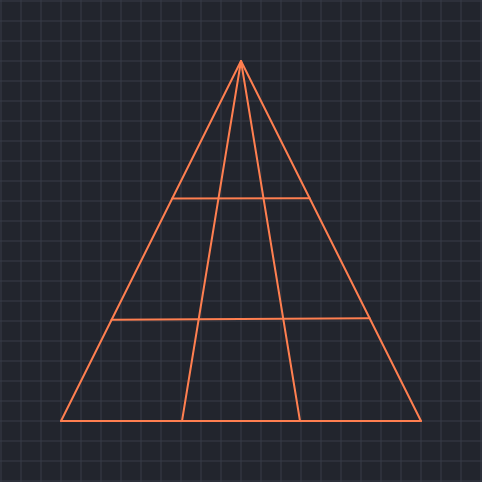 |  |  |
The first pattern has exactly 18 triangles:

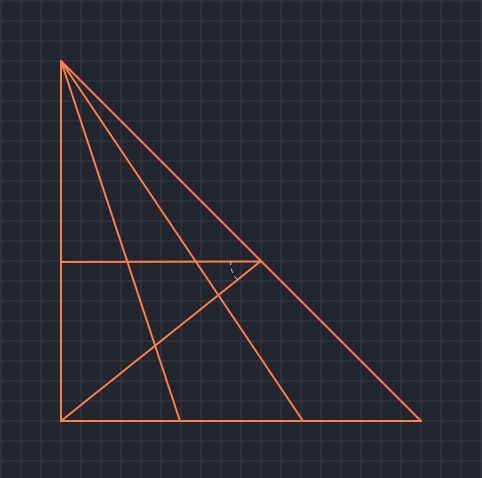
The second one has 24 triangles:

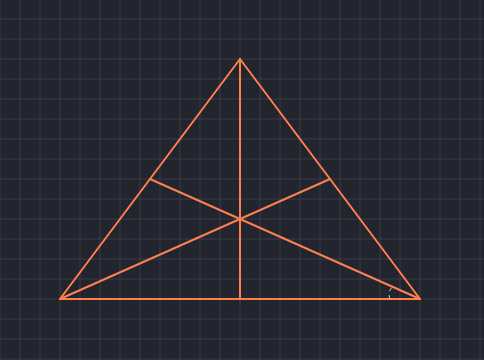
And, the last one has 16 triangles:

No doubt about it.
Oho, it seems like I am also claiming that my answer is the only correct answer 😀. But, no, I am not just claiming it, I actually applied a formula to these patterns which helped me figure out every single possible triangle hidden in the patterns.
Today, I will discuss that special formula. The formula which is the ultimate formula to figure out all the possible triangles in any type of pattern you think of.
Interesting, right? Yes, it is very easy but very powerful formula, even a primary school student will understand it.
So, let’s get started. 🎉
The Ultimate Formula:
As I have said the word “ultimate”, the formula must follow the brute-force method. Otherwise, it cannot be ultimate.
Yes, it is the brute-force method. What is the brute-force method? In short: This method is something that goes through all the possible values of something. Here, the word “Brute” is synonymous with “beast”, which means it works like a beast and doesn’t care about anything, and goes through every single possible value 🙂. Hope, you got it.
So,
For ease, I am presenting a sample pattern:

Step 1:
First of all, we have to find out all the intersection points in the pattern. We can name the points with numbers or letters. I recommend naming them with numbers.
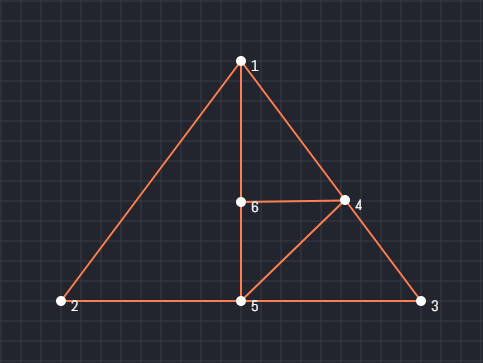
In the above sample pattern, we have got 6 intersection points.
Step 2:
Now, we have to find out all the possible triangles.
Before finding out the triangles, we have to list a sequence based on the brute-force method. To list the sequence, we can take a paper or an Excel sheet / Google sheet.
We would start listing from 123 according to the following rules:
Rule 1:
The number must be in 3 digits because a triangle consists of 3 intersection points. If it were about quadrilateral, the number would be in 4 digits because a quadrilateral has 4 intersection points.
Rule 2:
The number cannot have duplicate digits like 112, 344, 555, and so on. It should be like 236, 146, 245, and so on
Rule 3:
Every digit in the number must be larger than the previous one. For example: 274 is not correct. The correct version is 247. Here, 4 is greater than 2, 7 is greater than 4, and 2 is smaller than the others. This is why the first digit would be 2, then 4, and finally 7 🙂.
Rule 4:
The number cannot contain any digit that is larger than the total intersection points in the pattern. So, as the above sample pattern has 6 intersection points, the number should not contain any digit larger than 6.
So, we are going to start from 123, not from 111. Because if we start from 111, the above rules cannot be followed.
For example- 111, 112, 113, 114, 115, 116, 121, and 122. Here, every number breaks one or more of the above rules.
So, let’s start from 123:
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 123 | 234 | 345 | 456 |
| 124 | 235 | 346 | |
| 125 | 236 | 356 | |
| 126 | 245 | ||
| 134 | 246 | ||
| 135 | 256 | ||
| 136 | |||
| 145 | |||
| 146 | |||
| 156 |
You may have noticed that we stopped the above sequence every time when it reached 6 because there are no more points after 6, right? So, we cannot write 7 because 7 is greater than the total intersection points in the pattern and this point doesn’t exist.
Very easy, like a piece of cake!
Anyhow, now we would check visually all the numbers one by one in the sample pattern if they make triangles or not.
At First, 123:
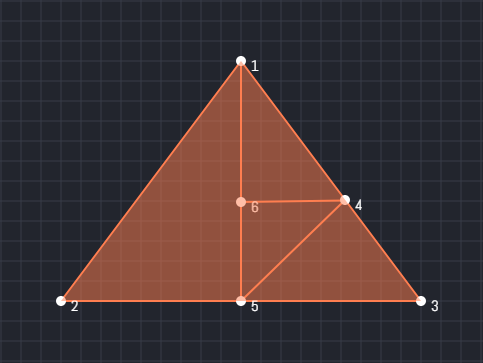
Is point 1 connected with point 2, point 2 is connected with point 3, and point 3 is connected with point 1? If so, it makes a triangle, right? So, we can mark this as a triangle.
Then, 124:
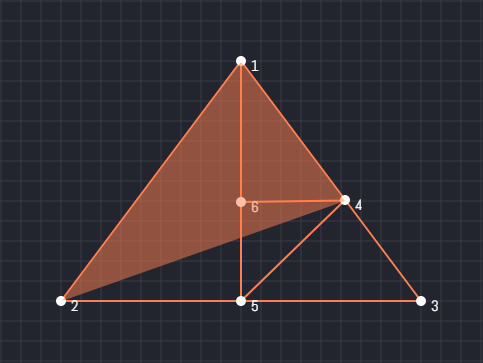
Is point 1 connected with point 2, point 2 is connected with point 4, and point 4 is connected with point 1? If so, it should make a triangle. We are seeing that points 1, 2, and 4 are not connected. So, it is not a triangle and we are not going to mark this.
It means if a number makes a triangle, we would mark that as follows:
| 1 | 2 | 3 | 4 |
|---|---|---|---|
| 123 ✅ | 234 | 345 ✅ | 456 ✅ |
| 124 | 235 | 346 | |
| 125 ✅ | 236 | 356 | |
| 126 | 245 | ||
| 134 | 246 | ||
| 135 ✅ | 256 | ||
| 136 | |||
| 145 ✅ | |||
| 146 ✅ | |||
| 156 |
Is it your expression now?-

Yes, it should be if you understand the matter 😀.
So, we have identified 7 triangles. It means there are exactly 7 triangles in the pattern.
And, they are 123, 125, 135, 145, 146, 345, and 456:
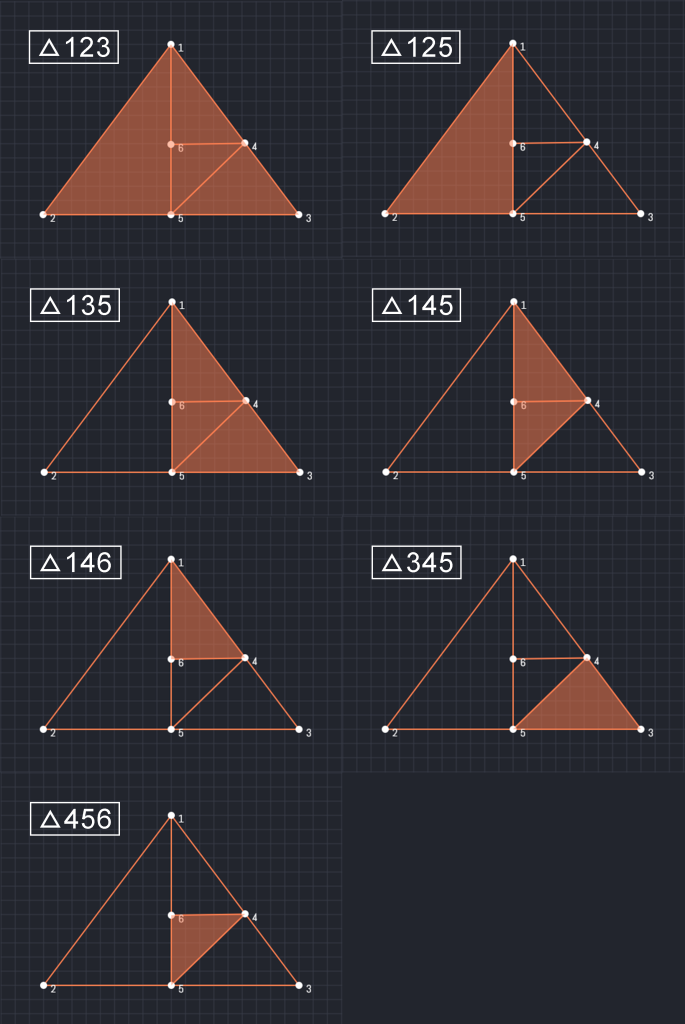
I hope I have been able to make everything crystal clear.
Any Online Tool?:
Now, it is the age of computers. There should be an app/tool that can count all the possible triangles quickly. So, I have made one which you can use to draw any type of pattern and count triangles within a few seconds 😃. Check out the tool here. The tool also shows the numbers of the intersection points and the arms of the drawn pattern.
Last But not the Least:
If you found the article helpful, don’t forget to let us know by comment.
Thank you!

![How Many Triangles are There [Ultimate Formula] How Many Triangles are There [Ultimate Formula]](https://shapecounter.gsghalib.com/wp-content/uploads/2024/12/How-Many-Triangles-are-There-Ultimate-Formula.png)
0 Comments